Kontakty:
doc. RNDr. Peter Papp, PhD., F2-46, peter.papp AT uniba.sk (prednášky)
Mgr. Dominika Melicherová, PhD., F2-241, dominka.melicherova AT fmph.uniba.sk (cvičenia)
Mgr. Filip Pastierovič, F2-148, filip.pastierovic AT fmph.uniba.sk (cvičenia)
Cieľ predmetu:
- Numericky vyriešiť niektoré základné fyzikálne problémy (väčšina z nich nemá analytické riešenie).
- Naučiť sa základné algoritmy riešenia fyzikálnych úloh.
- Naučiť sa napísať jednoduché programy, spracovať a vyhodnotiť získané výsledky.
- Oboznámiť sa s niektorými fyzikálnymi javmi, ktoré sa (možno) v základných prednáškach nespomínajú.
Rozsah predmetu:
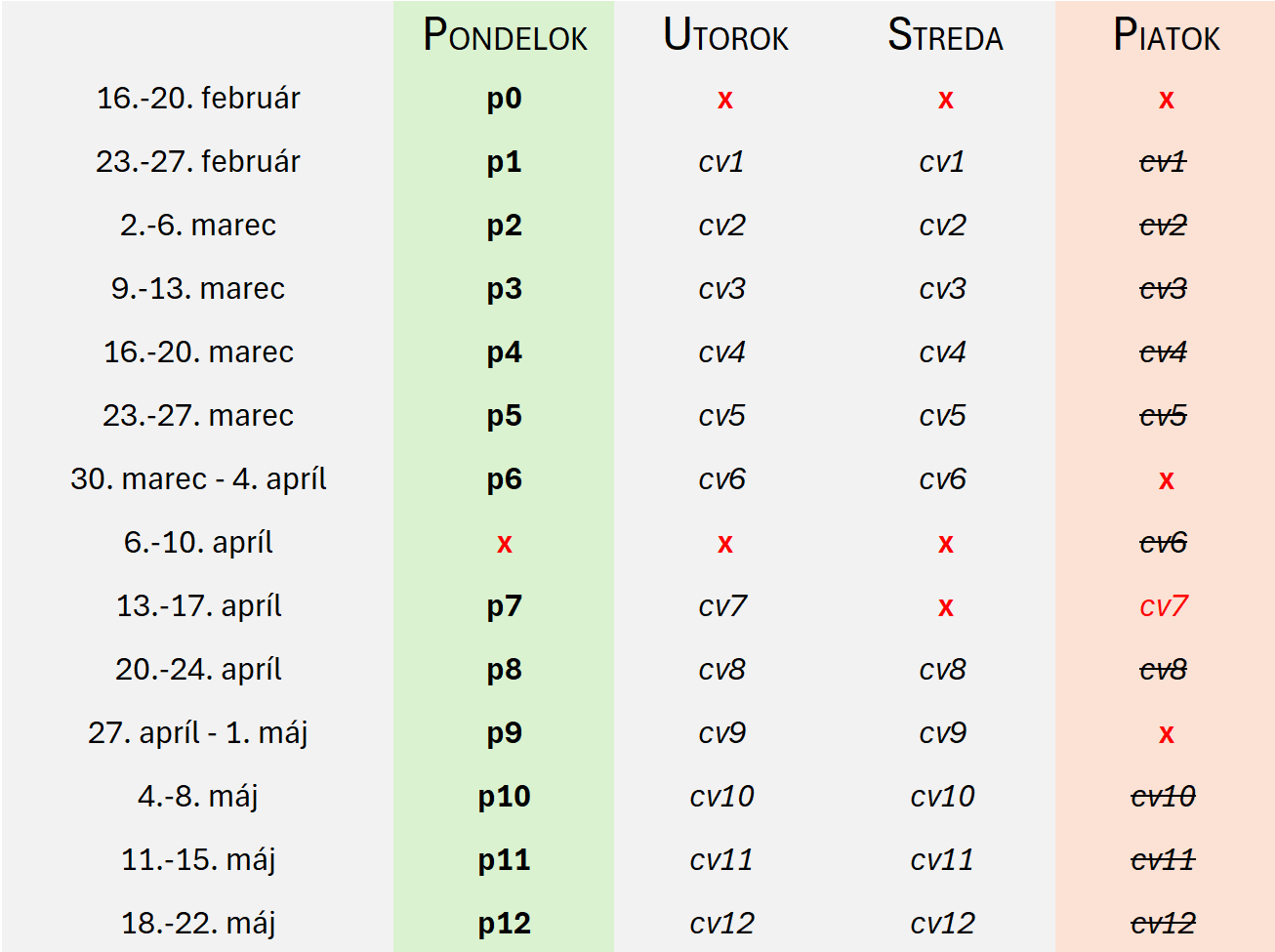
- v roku 2026 bude 12 prednášok (45 minút) na 13 rôznych tém, 12 cvičení na prípravu úloh (90 minút),
- v roku 2026 odpadá cvičenie 3. apríla, prednáška 6. apríla a cvičenie 7. apríla (Veľkonočné sviatky a s nimi súvisiace dekanské a rektorské voľná), cvičenie 15. apríla (celofakultné kolo ŠVK), cvičenie 1. mája (štátny sviatok)
- po vzájomnej dohode je nateraz piatkové cvičenie zrušené a študenti sa rozdelia do dvoch skupín v utorok od 14:50 a stredu od 15:40, ak to ale nebude udržateľné z kapacitných dôvodov, piatkové cvičenie bude obnovené
- 7. cvičenie plánované na 15. apríla bude nahradené výnimočne v piatok 17. apríla
- ku každej téme bude na konci prednášky zadaná úloha – vypracovať jednoduchý program podľa zadania v prezentácii,
- voľba programovacieho jazyka je na študentovi (C++, Python…),
- v niektorých prezentáciách je uvedených viac úloh, vtedy stačí odovzdať len jednu z nich,
- úlohy odporúčame konzultovať a vypracovať priamo na cvičeniach, kde za ne dostanete aj bodové ohodnotenie,
- kto nestihne úlohu dokončiť na cvičení, má možnosť ju dokončiť a odovzdať do nasledujúcej hodiny,
- študenti musia odovzdať program cvičiacemu mailom (zdrojový kód, povinne),
- minimálny bodový zisk na absolvovanie predmetu je 50 bodov:
- A ≥ 90% > B ≥ 80% > C ≥ 70% > D ≥ 60% > E ≥ 50% > Fx
- študenti, ktorí nezískajú za úlohy vypracované na cvičeniach minimálne 50 bodov, musia preukázať autorstvo zdrojových kódov na osobnej konzultácii v skúškovom,
- úlohy sú rozdelené na 5 A-čkových a 8 B-čkových, výsledná známka sa vypočítava na základe tabuľky nižšie
Hodnotenie predmetu:
- výsledná známka sa vypočítava na základe súčtu bodov za odovzdané úlohy A kategórie (minimálne 3 bezchybné) a B kategórie:
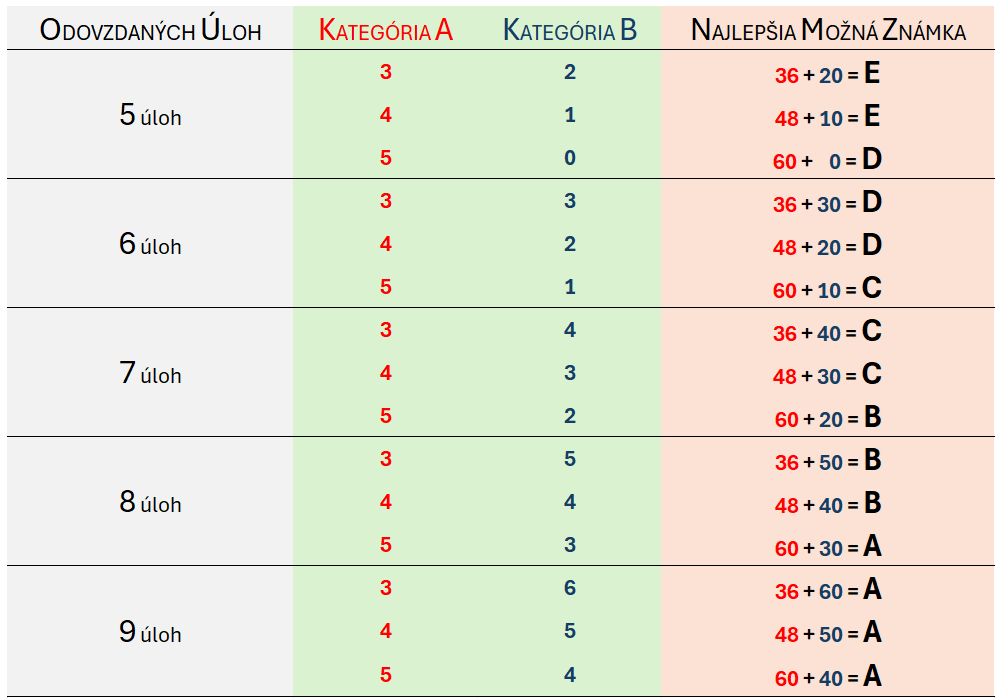
Harmonogram a materiály 2026, rozdelenie úloh do kategórií A a B:
| Termín prednášky | Číslo a popis úlohy, prezentácia z prednášky | Termín odovzdania úlohy |
| 23.2.2026 | B01 – Numerická stabilita jednoduchých iteračných schém – Zlatý rez, prechod od spojitého problému k diskrétnemu. | |
| 2.3.2026 | B02 – Nelineárne iteračné schémy – Phase locking, period doubling, intermitencia, prechod ku chaosu. Výpočet pravdepodobnostného rozdelenia, fraktálnej dimenzie. Ukážka niektorých Fraktálov a multifraktálov vo fyzike. | |
| 9.3.2026 | A03 – Náhodné čísla – Pravdepodobnostné rozdelenia: Poissonovo (náhodné delenie intervalu) a Gaussovo rozdelenie – zákon veľkých čísiel. Zoradenie čísiel, numerická konštrukcia pravdepodobnostného rozdelenia. | |
| 16.3.2026 | A04 – Integrály – Perióda nelineárneho kyvadla. Algoritmy výpočtu určitého integrálu. Klasické ortogonálne polynómy. Error function. Nuly a váhy Gauss-Legendreovho polynómu pre N=64 | |
| 23.3.2026 | B05 – Numerické riešenie vlnovej rovnice – Prechod vlny planárnou dielektrickou vrstvou – výpočet koeficientu prechodu). Presnosť výpočtov. Rezonančné tunelovanie cez dve kovové vrstvy. | |
| 30.3.2026 | A06 – Diferenciálne rovnice – Metódy Runge-Kutta. Systémy diferenciálnych rovníc. Harmonický oscilátor. | |
| 13.4.2026 | B07 – Metóda streľby – Výpočet vlastných frekvencií a vlastných stavov viazaných sústav: struna pevne ukotvená na koncoch, elektromagentické pole v tenkej dielektrickej vrstve. Vlastné energie a vlastné stavy viazaných kvantových systémov: kvantového harmonického oscilátora, dvojitej potenciálovej jamy. | |
| 20.4.2026 | A08 – Elektrostatika v 1D a 2D – Elektrostatický problém rozloženia náboja na kovovom telese. Jednoduchá integrálna rovnica. Riešenie systému lineárnych rovnic, Gauss-Jordanova metóda. Numerická inverzia matice. | |
| 27.4.2026 | B09 – Minimalizácia, optimalizácia – Hľadanie minima funkcie jednej premennej a funkcie mnohých premenných (simplex). Fitovacie procedúry, odhad chyby fitovacích parametrov. Programy (vo fortrane) pre minimalizáciu: jednorozmernú a pre simplex (minimalizácia funkcie N premenných). | |
| 4.5.2026 | A10 – Diagonalizácia – Numerická diagonalizácia matíc. Vlastné hodnoty a vlastné vektory symetrickej matice (Jacobiho metóda diagonalizácie). Iteračná metóda hľadania vlastných hodnôt matice, Schmidtova ortonormalizácia. Atóm vodíka. Vlastné hodnoty a vlastné vektory nájdené metódou diagonalizácie matice. | |
| 11.5.2026 | B11 – Glauberova dynamika v spinových systémoch – Dvojrozmerný Isingov model. Glauberova dynamika.(príkazy pre gnuplot). Vstupný file obsahuje v riadkoch hodnotu x, y, s(x,y) s prázdnym riadkom po každom stĺpci. | |
| 18.5.2026 | B12 – Diferenciálne rovnice II – Použitie metód Runge-Kutta. Budený hamonický oscilátor s tlmením, Nelineárne kyvadlo. | |
| samoštúdium | B13 – Rýchla Fourierova transformácia FFT – Programy (vo fortrane) pre obyčajnú a rýchlu Fourierovu transformáciu. |
Literatúra:
- P. Markoš: Počítačová fyzika. Skriptá k preberanej látke
- W. H. Press, S. A. Teukolsky, et al.: Numerical Recipes. Cambridge Univ. Press, 1992
- E. Vitásek, Numerické metody. SNTL Praha 1987